Ezen a ponton, a betűírás kialakulásával veszi kezdetét a titkosírások (ismert) története. A korábbi időszakokból egyáltalán nem ismerünk titkosírásokat (jóllehet a Phaisztoszi korongról ez irányú munkásságom kezdetén éppen azt feltételeztem, hogy lényegében egyfajta titkosírás). Ez tulajdonképpen furcsa, mivel az újkori titkosírások története azt mutatja, hogy a megszületéséhez fejlett bürokrácia, kényes politikai helyzetek és kiterjedt katonai hírszerzés szükséges, amely feltételeknek már az Ókori Közel-Keleten is számos történeti kor eleget tett. A titkosírás filozófiája a betűírások korában az, hogy a nyelv hangjai azonosak azzal a jellel, amelyet az írástanulás során az ember elsajátított, következésképpen ha ezt egy másik jellel helyettesítjük, senki más nem fogja megérteni (a kriptográfia voltaképpen éppen azzal a felismeréssel veszi kezdetét, hogy egy nyelv hangzását a megszokottól eltérő jelek alkalmazása nem rejti el, hanem éppenhogy ugyanúgy tükrözi). Miért ne alakulhatott volna ki ez az elképzelés a szótagírások korszakában, amikor egyébként a titkosítás igénye az egyéb követelmények alapján már megszülethetett volna?

Az első ismert rejtjelezési módszer ismertetése Julius Caesar korára vonatkozik, de tudomásom szerint a klasszikus ókorból sem ismerünk fennmaradt titkosírásos emlékeket. Az arab kriptográfia már a 9. században olyan fejlett volt, hogy a megfigyeléseinek mindenképpen kiterjedt titkosíráshasználati gyakorlatra kellett alapulnia, nem vagyok azonban biztos abban, hogy ismerünk-e egyáltalán fennmaradt arab titkosított szövegeket? Ha valóban hiányoznak az ilyen dokumentumok, akkor vajon nem feltételezhetjük-e teljes joggal, hogy a rejtjelezés sokkal nagyobb múltra tekint vissza, mint amit ismerünk?

A témánk szempontjából mindez azonban kevésbé lényeges. A fontos az, hogy illusztráljuk azt, hogy mennyire logikus kapcsolat van a nyelvfogalom alakulása/átgondolása és az információ nyilvánossá tétele/elrejtése közt.

Azt a naiv elképzelést, hogy a hang és a jelölésére alkalmazott grafikus jel iskolában megtanult, és egyértelműnek vélt összefüggését „kicselezve” mások által értelmezhetetlen írást alakíthatunk ki, az arab kriptográfia már a 9. században megcáfolta a gyakoriságelemzés módszerével. Minderről Európában semmit sem tudtak, azonban a 14. század végén a kontinensünkön is (elsősorban Itáliában) megindult a kriptográfia lassú fejlődése. A rejtjelezés a mai szemmel nézve még gyerekcipőben járt 1430 körül, ezért olyan érthetetlen és bosszantó, hogy a kb. ekkor keletkezett, látszólag monoalfabetikus (egyábécés) titkosírással írt ún. „Voynich-kódex” miért áll ellen a mai napig a legkiválóbb szakértők megfejtési kísérleteinek.

A 14. század végén tehát Európában is elkezdődött a gondolkozás a nyelv és az írás viszonyáról. Nem filozófusok és tudósok kezdtek azonban töprengeni kezdetben a kérdésről, hanem írnokok, hivatalnokok próbálták meg a maguk gyakorlatias felfogásával és ösztönös nyelvfelfogásuk alapján biztosabbá tenni a rejtjelezett szövegeket. A magánhangzók azonosításához minimális logika is elegendő (mind statisztikai-, mind pozícióanalízissel kimutathatók) ha az ember már el tud szakadni a betanult „egy jel = egy hang” azonosítástól, és természetesen, ha már maga is készített monoalfabetikus (egyábécés) titkosírást. Az ösztönös megoldás ennek a kivédésére az, hogy a magánhangzók helyett nem egy, hanem több jelet alkalmazunk.

Titkosírás létrehozóiként látszólag meg is elégedhetnénk ezzel a módszerrel, ám nyilvánvaló, hogy ha a feladatunk már nem egy ilyen titkosírás kitalálása, hanem egy ugyanilyen módszerrel titkosított szöveg megfejtése, akkor a saját csapdánkba estünk! Ebben az esetben újabb ötletekre van szükségünk – nyilvánvalóan a többi jel, a mássalhangzók elemzésére. Egy kis gondolkodásra lesz szükség hozzá, de nyilvánvaló, hogy a leggyakrabban előforduló jelekben nem az x, y, vagy a q betűket keressük (persze ezt is nyelve váltogatja), hanem az írásban legtöbbször előforduló mássalhangzókat. Ennek során a rejtjeles írás elemzője rájön arra, hogy az általános gyakoriságelemzéssel könnyen azonosíthatók egy nyelv hangjai (mint láttuk, a magánhangzókat nem jelölő arab írás környezetében erre már évszázadokkal korábban rájöttek). Ösztönös megoldása tehát az lesz, hogy (legalább is a leggyakoribb) mássalhangzók jelölésére is több jelet használ. Megfejtőként pedig majd ismét arra kell rájönnie, hogy a „saját maga” által kitalált módszerrel kialakított ismeretlen titkosírást vajon hogyan fejtse meg?

A modern titkosírások dinamikus fejlődését éppen ez az „ördögi kör” lendítette előre, magával vonva a nyelvről való gondolkodás ösztönös, a speciális igényekre korlátozódó fejlődését is. Mivel az ugyanarra a hangra alkalmazott különböző grafikus jeleket a görög nyelv segítségével kialakított szakszóval „homofónoknak” nevezzük, az ilyen titkosírásrendszereket homofónikus írásoknak hívjuk.

A gyakorlati titkosíráshasználat tulajdonképpen nagyon jól elboldogult volna ezzel a rejtjel-szisztémával a nyelvi alapokon való elmélyültebb gondolkodás nélkül is (mint ahogy a valóságban tényleg évszázadokig ez volt a titkosírások rendszere), mivel egészen nagy biztonságot lehet elérni az alkalmazásával (a „Zodiákus” nevű sorozatgyilkos ilyen elvekre épülő titkosírásainak egy része pl. még a mai napig megfejtetlen).

Amint azonban tudósok, gondolkodók érdeklődését is felkeltette a rejtjelezés, a kriptográfia teoretikus lehetőségei is virágzásnak indultak. Johannes Trithemius elméleti javaslataiban pl. egyrészt a „homofónikus” gondolat „túlburjánzása” figyelhető meg, a szerző a 16. század elején már olyan írástervezeteket alakított ki, amelyben minden betűnek kb. 100 homofón felelt meg. Egy homofónikus írás természetesen annál kevésbé fejthető meg a gyakoriságelemzés alapján, minél több homofón jelöli ugyanazt a betűt, ugyanakkor nem biztos, hogy a(z ilyen jellegű) titkosírás hatékonysága is feltétlenül ettől fog függeni, hiszen minél jobban növeljük ezt a számot, annál bonyolultabb kódfejtő „szótárakra”, táblázatokra lesz szüksége nemcsak a kódolónak a megszövegezés során, de nyilván a dekódolónak is. Matematikailag valószínűleg kiszámítható lenne, hogy a használhatóság szempontjából melyik a legoptimálisabb homofón-szám (és ez feltehetőleg a nyelvben elfoglalt gyakorisága alapján ráadásul minden jelnél egyedileg változna).

Egy ilyen jellegű „túlkapás” valószínűleg teljesen a feledés homályába merült volna, ha Trithemiusnak nem lett volna „mellékesen” az az ötlete, hogy a homofónokat ne egyetlen jel, hanem egy egész szó helyettesítse; így az ötlete valójában nem is egy homofónikus, hanem egy ún. szteganografikus (elrejtő) titkosírás lett, mivel az egyes betűket jelölő kb. 100-100 rejtjelből már egy „kvázi” értelmes, gyanakvásra semmi okot nem adó „fedőüzenetet” lehetett kialakítani (egyik rendszerében latin szavakat használt erre a célra, amelyek valóban alkalmasak lehettek volna a rejtjelezett tartalom elfedésére; egy másikban viszont értelmetlen, „mágikus” szóalakokat – mely utóbbiak pedig természetesen inkább az azonnali gyanakvást válthatták ki az üzenet olvasójából).

Hasonló gondolat (ti. az egy betűhöz rendelhető homofónok számának radikális megnövelése) vezethette a sokoldalú humanista Leon Battista Albertit is, amikor 1470 körül lefektette az ún. polialfabetikus (többábécés) rejtjelezés alapjait. Az elv nagyon egyszerű, és egyszerűségében is zseniális: ha már minden hang jelölésére több jelet alkalmazunk, miért ne használhatnánk az ábécé összes betűjére (hangjára) ugyanazt a karakterkészletet: az ábécé összes betűjét? Ebben az esetben nem kell újabb és újabb jeleket bevezetnünk, hanem megelégedhetünk a meglévőkkel, viszont a homofónokat olyan rendszerbe kell foglalnunk, hogy véletlenül se okozhassanak kétértelműségeket a behelyettesítésben. Hogy ez pontosan mit jelent, azt leginkább a rendszer továbbfejlesztőinek táblázatai mutatják szemléletesen. Alberti még az inkább gyakorlatias „rejtjelező korongot” használta (egy kisebb és egy nagyobb, egymáson elforgatható korong, amelyeknek a szélein egy-egy ábécé volt található).

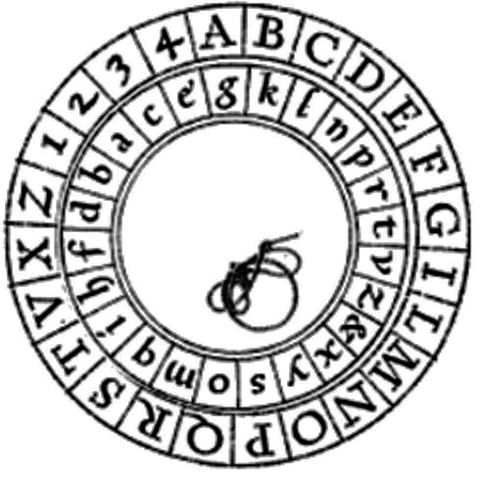
Alberti még rövid szakaszonként váltogatta a rendszerbe foglalt behelyettesítéseket, az ún. (ábécé)„eltolásokat”, azonban nyilvánvaló, hogy ezek a rövid, önmagukban azonos rejtjelezéssel írt szakaszok támpontokat nyújthattak volna annak a kódfejtőnek, aki esetleg ismeri az eljárás lényegét. A fentebb már említett Johannes Trithemius emiatt már minden egyes betűt az egymás után következő ábécé-eltolásokkal kódolt, azonban ez még mindig túl szisztematikusnak tűnt az elméleti kriptográfusok számára, ezért Blaise de Vigenère felszámolta az elődei ilyesfajta rendszerességét, és egy tetszőlegesen megválasztott „kulcsszó” betűinek a(z esetleges) pozíciója és sorrendje alapján határozta meg az aktuális betű behelyettesítését.

Lényegében ezt az elvet fejlesztették tovább a hírhedt Enigma, és a hasonló rejtjelező gépek egészen a legmodernebb titkosítási rendszerekig, azonban a rejtjelezésnek ez a története már annyira absztrakt, hogy semmiféle párhuzamot nem mutat a természetes írásfejlődéssel, ahogyan a számtalan további lehetőség sem (pl. a híres Cardano-féle rejtjelrács, vagy a kémtörténetekből ismert „könyvkód” stb.).

Érdemes azonban itt kitérnünk arra is, hogy a polialfabetikus rejtjelezés általános megfejtését végül mégis a nyelvi jellegzetességek alapján sikerült kidolgozni (amire a kitalálói bizonyára álmukban sem gondoltak volna, holott utólag rendkívül logikusnak tűnik). A Vigenère rejtjelben először is a kulcsszó hosszát kell megállapítani. Nyilvánvaló ugyanis, hogy pl. egy hatbetűs kulcsszó esetében az 1., 7., 13., 19. ...; a 2., 8., 14., 20. …; a 3., 9., 15., 21. … stb. betűk ugyanazzal az egyábécés (monoalfabetikus) titkosírásokkal vannak kódolva. Kellő hosszúságú szöveg esetén az is törvényszerű, hogy a leggyakoribb hármas betűcsoportok (gondoljunk pl. az angol „the” névelőre) időnként ugyanazon a három egymást követő „eltoláson” vannak rejtjelezve (pl. az egyik hármas a kulcsszó 2-3-4., a másik a 4-5-6., egy harmadik pedig a 3-4-5. stb. betűjének megfelelő eltolás szerint van kódolva). Ha tehát megszámoljuk az ilyen ismétlődő hármasok közötti távolságot, és azt találjuk, hogy az egyik pl. 12 és 36, egy másik 18 és 42 stb. pozícióra van egymástól, gyanakodhatunk, hogy a kulcsszó 6 betűs. Ha mármost a szöveget feldaraboljuk, és a kulcsszó logikája szerinti 6 különböző csoportba rendezzük, mindössze 6 monoalfabetikus titkosírást kell „megfejtenünk”, azaz az így kapott 6 különböző jelgyakoriságot kell azonosítanunk a feltételezett nyelv gyakorisági mutatóival (első pillantásra talán hihetetlennek tűnik, hogy egy így összeszabdalt, önmagában teljesen értelmetlen jelsorozat is ugyanazt a jeleloszlást fogja mutatni, mint egy értelmes szöveg, azonban ha belegondolunk, kellő hosszúságú szöveg esetében a „nagy számok törvénye szerint” valóban ennek az eredménynek kell kijönnie), és ezzel megkapjuk azt a 6, „eltoláson” alapuló egyábécés titkosírást, amely szerint a rejtjel kódolva van. (Létezik azonban ennek a módszernek egy elméletileg is megfejthetetlen változata, amikor a kulcsszó magával a rejtjelezett üzenettel azonos, azaz a következő rejtjel pozícióját mindig az éppen aktuális kód határozza meg; ez az ún. „végtelen átkulcsolás” vagy „futókulcs”.)

Érdekességként pedig érdemes azt is megemlíteni, hogy Vámos Hanna a közelmúltban egy, a Trithemius-rendszer egy változatával (a rejtjelezés rendszere minden szó elején újrakezdődött) kódolt magyarországi titkosírást egy fejezetcím (és a nyelv, valamint a szisztéma helyes feltételezése) alapján lényegében néhány perc alatt megfejtett!

A homofónikus titkosírásoktól tettük ezt a kis kitérőt annak érzékeltetésére, hogy hová vezethet a homofónia-elv következetes alkalmazása. A homofónikus elnevezés ugyanakkor ezeknek a rejtjelezési rendszereknek csak az egyik, nem kizárólagos, de legjellemzőbb sajátosságát adja vissza. A magánhangzók könnyű azonosíthatósága (és az egyre nyilvánvalóbbá váló gyakoriságelemzés lehetősége) mellett természetesen az írásfejtő gyakorlat hamarosan kialakította a maga ellenszereit: a kettőshangzók azonosítása ellen külön jelet vezetett be ezekre, a nyelvre jellemző gyakori hangzócsoportok felismerése ellen a különböző szótagjeleket, a címzett, a küldő, vagy csak a gyakrabban hivatkozott személyek, városok mintázatának könnyű felfedezése ellen pedig a szójeleket, az ún „nomenklátorokat” (a nomenclatorok – lat. 'névkiáltók' – eredetileg azok a szolgák voltak, akik az ünnepségeken a vendégek teljes címét felolvasták; idővel a neveket és titulusokat könnyen megjegyezhető szimbólumokkal helyettesítették, és kézikönyvekben is összefoglalták – ld. Paul Lunde: Titkos kódok. Kossuth Kiadó, Budapest, 2010, 70.), és a gyakoriságelemzés megnehezítésére – úgy általában – a semmit nem jelentő, ki nem olvasandó karaktereket, az ún. „nullitásokat” (nullitásokat pl. a szóközök helyett is lehet alkalmazni, amivel természetesen „pokollá” tehetjük a kódfejtő tevékenységét).

Egy homofónikus titkosírás közelmúltbeli megfejtése (melyben a magyar származású Megyesi Beáta is részt vett) azonban azt bizonyította, hogy van olyan módszer, ami a heterogén rendszer elemeit képes szétválasztani típusaik szerint. A titkosírás jeleinek környezetvizsgálata ugyanis egy olyan diagramot eredményezett, amin elkülönült csoportokba rendeződtek a később nomenklátoroknak, nullitásoknak, valamint magán- és mássalhangzóknak bizonyuló jelek, a homofónok pedig egymás közvetlen szomszédságába kerültek (L = nomenklátorok, D = mássalhangzó duplázását jelző jel, e- = en/em, azaz nazális e; a szóközök = nullitások).

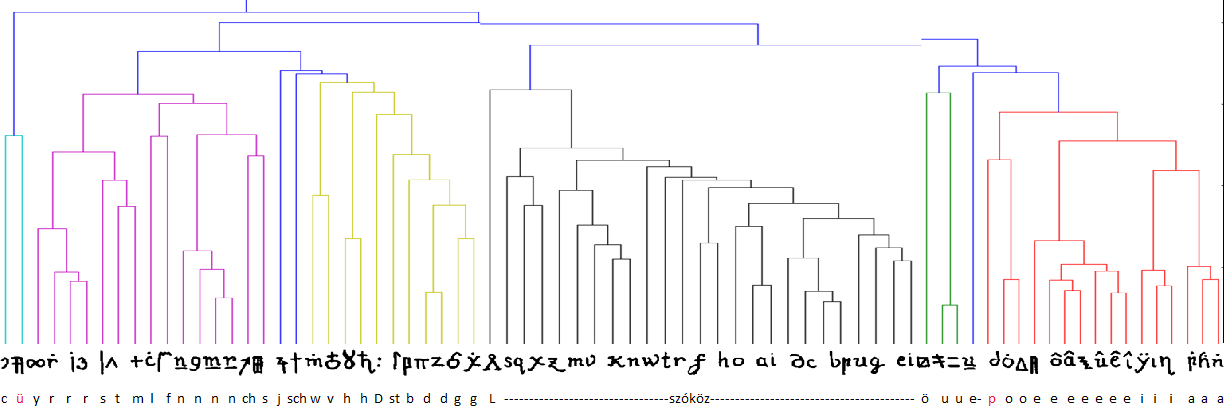
Ez a rendszer bonyolultságával feltűnően emlékeztet az egyiptomi és mezopotámiai írásokra, amelyek szintén egyszerre használtak ki nem olvasott (nem hangzó) jelentéspontosító jeleket (determinatívumokat), szójeleket, szótagjeleket (ill. kettős- vagy hármas mássalhangzókat az egyiptomiban) és betűjeleket (az egyiptomiban). Nyilvánvaló természetesen, hogy a hasonlóság csak véletlenszerű; azonban egyáltalán nem az, ha a két írástípus írásfejlődési rendszerekben elfoglalt helyét tekintjük. Mert amíg ez utóbbi írások (konzervativizmusuk miatt) köztes pozíciót foglalnak el a tisztán fogalomjelölő írás tisztán fonetikus típusba való átalakulása között, addig a homofónikus rejtjelek ugyanebben a pozícióban találhatók a tisztán hangjelölő egyábécés (monoalfabetikus), és a teljes egészében fogalomjeleket használó modern kori kódírás közt – a bonyolultságot itt pedig (elméleti szinten) a következetes át nem gondoltság és (gyakorlati szinten) a praktikus alkalmazhatóság magyarázza. És ahogy az íráshagyományokkal nem „terhelt” népek kiszűrik a „fölösleges” jeleket ebből a rendszerből, lényegében szótagírásra – ill. a sémi népeknél betűírásra – redukálva a szisztémát (a pontosság kedvéért tegyük azonban hozzá, hogy kisebb számban ugyan, de még a krétai és hettita írások is alkalmaznak determinatívumokat és ideogrammokat), úgy a homofónikus rejtjelezésben is megvan annak a lehetősége, hogy következetesebb átgondolással a sokféle elemből kiszűrjék a fölöslegesnek gondoltakat. A homofónikus titkosírások közül ugyan tudtommal egy sem vált tisztán nomenklátorokat használó kódírássá (azonban a nomenklátorok száma egyre nőtt, és XIV. Lajos korára már nem volt ritka a közel ezer tételt tartalmazó kódszótár sem – ld. Láng Benedek: A Rohonci kód. Jaffa Kiadó, Budapest, 2011, 103. –, egy 1300 tételes kódtábla a korszak egyik legnagyobb nomenklátorszótárával pedig az 1664-68 közötti magyar vonatkozású anyagban található egy bécsi levéltárban – Láng Benedek: Titkosírás a kora újkori Magyarországon. Balassi Kiadó, Budapest, 2015, 78.), valószínű viszont, hogy az alkotóelemei arányának radikális eltolásával alakította ki XIV. Lajos híres kriptográfusa, Antoine Rossignol az ún. „Grand Chiffre”-t (Nagy Rejtjel), amely kizárólag szótagokat használt a kódolásra.

A bejegyzés folytatása két nap múlva kerül fel a blogra.

A bejegyzés trackback címe:

Kommentek:

A hozzászólások a vonatkozó jogszabályok  értelmében felhasználói tartalomnak minősülnek, értük a szolgáltatás technikai  üzemeltetője semmilyen felelősséget nem vállal, azokat nem ellenőrzi. Kifogás esetén forduljon a blog szerkesztőjéhez. Részletek a  Felhasználási feltételekben és az adatvédelmi tájékoztatóban.